Physical Quantities and Measurement – Exercise Questions

(c) Newton

(d) watt

iii. Amount of a substance in terms of numbers is measured in:   (LHR 2011)

(a) Gram

(b) kilogram

(c) Newton

(d) mole ✔

iv. An interval of 200 µs is equivalent to:    (LHR 2015)

(a) 0.2 s

(b) 0.02 s

(c) 2 x 10^-4 s ✔

(d) 2 x 10^-6 s

v. Which one of the following is the smallest quantity?

(a) 0.01 g

(b) 2 mg

(c) 100 µg

(d) 5000 ng ✔

vi. Which instrument is most suitable to measure the internal diameter of a test tube?

(a) Meter rule

(b) Vernier callipers ✔

(c) Measuring tap

(d) screw gauge

vii. A student claimed the diameter of a wire as 1.032 cm using Vernier calipers. Up to what extent do you agree with it?

(a) 1 cm

(b) 1.0 cm

(c) 1.03 cm ✔

(d) 1.032 cm

viii. A measuring cylinder is used to measure:

(a) Mass

(b) area

(c) Volume ✔

(d) level of a liquid

ix. A student noted the thickness of a glass sheet using a screw gauge. On the main scale, it reads 3 divisions while 8th division on the circular scale coincides with index line. Its thickness is:

(a) 3.8 cm

(b) 3.08 cm

(c) 3.08 mm ✔

(d) 3.08 m

x. Significant figures in an expression are:

(a) All the digits

(b) All the accurately known digits

(c) All the accurately known digits and the first doubtful digit ✔

(d) All the accurately known and all the doubtful digits

xi. Identify the base quantity in the following:

(a) Speed

(b) Area

(c) Force

(d) Distance ✔

 

1.2       What is the difference between base quantities and derived quantities? Give three examples in each case.

Base Quantities	Derived Quantities
The quantities on the basis of which other quantities are expressed are known as base quantities. Examples Length, time, mass	Physical quantities which can be described in terms of base quantities are known as derived quantities. Examples Force, area, volume

 

1.3       Pick out the base units in the following:

Joule, Newton, kilogram, hertz, mole, ampere, meter, Kelvin, coulomb and watt.

Base units

• Kilogram (unit of mass)
• Mole (unit of quantity of substance)
• Ampere (unit of electric current)
• Metre (unit of length)
• Kelvin (unit of temperature)

 

1.4       Find the base quantities involved in each of the following derived quantities:

(a) Speed                     (b) Volume                 (c) Force                    (d) Work

Ans:    (a) Speed

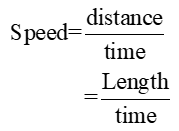
So base quantities involved in speed are length and time.

           

(b) Volume:

Volume = length × width × height

= length × length × length

So base quantities involved in volume is length.

 

(c) Force:

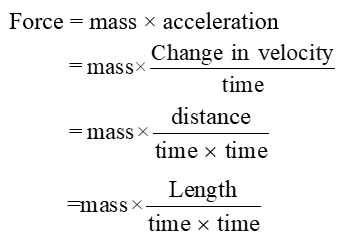
So base quantities involved in force are length mass and time.

 

(d) Work:

So base quantities involved in work are length, mass and time.

 

1.5       Estimate your age in seconds.     (LHR 2014, 2015)

Ans:    Let present age = 15 years

= 15 × 365 days

= 5475 days

= 5475 × 24 hours

= 131400 hours

= 131400 × 3600 second

= 473040000 second 

 

1.6       What role SI units have played in the development of science?    (LHR 2013)

Ans:    With the development in the field of science and technology, the need for a commonly acceptable system of units was seriously felt all over the world particularly to exchange scientific and technical information. To fulfil this need a world-wide system of measurements called international system of units was adopted.

 

1.7       What is meant by vernier constant?     (LHR 2014, 2015)

Ans:    “The difference between one small division on main scale and one vernier scale division is called vernier constant. This is the minimum length which can be measured accurately with the help of a vernier callipers. That is why it is also called the least count of vernier callipers”.

 

1.8       What do you understand by the zero error of a measuring instrument? (LHR 2014)

Ans:    The error in a measuring instrument due to non-uniform or wrongly marked graduation due to which a measurement may be less or greater than actual measurement is called zero error of the measuring instrument.

 

1.9       Why is the use of zero error necessary in a measuring instrument?    (LHR 2013)

Ans:    If a measuring instrument has a zero error, readings taken by it will not be correct. By knowing the zero error first, necessary correction can be made to find the correct measurement. Such a correction is called zero correction.

 

1.10       What is a stopwatch? What is the least count of a mechanical stopwatch you have used in the laboratories?

Ans:    “An instrument used to measure the time interval or specific period of an event is known as stop watch”. Least count of mechanical stop watch is 0.1 second.

 

1.11       Why do we need to measure extremely small interval of times?

Ans:    We need to measure extremely small interval of times to get accurate and error free results of experiments.

 

1.12       What is meant by significant figures of a measurement?   (GRW 2013)

Ans:    In any measurement all the accurately known digits and first doubtful digit is known as significant figure.

 

1.13       How is precision related to the significant figures in a measured quantity?

Ans:    An improvement in the quality of measurement by using better instrument increases the significant figures in the measured result. More significant figure means greater precision. E.g. measurement of vernier callipers would be more precise than a metre rule, therefore measurements taken by vernier callipers would have more significant figures than that taken by metre rule.

» View Less